Observing Time
For heterodyne observations, estimate the sensitivity with the radiometer equation:
- Trms = K Tsys (t ∆f )-1/2,
where Tsys is the system temperature, t is the integration time, ∆f is the channel width, and K ≈ 2, depending on the switching scheme and observing strategy. Invert this equation to estimate the necessary observing time. Do not neglect to add overhead for setup, pointing, calibration, etc.
System Temperature
Estimate system temperature on the TA* scale with:
- Tsys [SSB, TA*] = [exp(τA ) / α] × 2 × (Trx [DSB] + α [1 - exp(-τA )] Tatm + (1 - α ) Tspill ) ,
where
- τ is the atmospheric optical depth at the observing frequency, see model atmospheric spectra,
- A is the airmass = secant (zenith angle),
- α is the hot spillover efficiency = 1 - (fraction of power falling on ground, etc.), ≈ 93%,
- Tatm is the atmospheric temperature, ≈ 280 K,
- Tspill is the warm spillover temperature, ≈ 280 K, and
- the Cosmic (Microwave) Background Radiation has been ignored.
For the above parameters and TRx = 40 K [DSB], the approximate SSB system temperature at 230 GHz is:
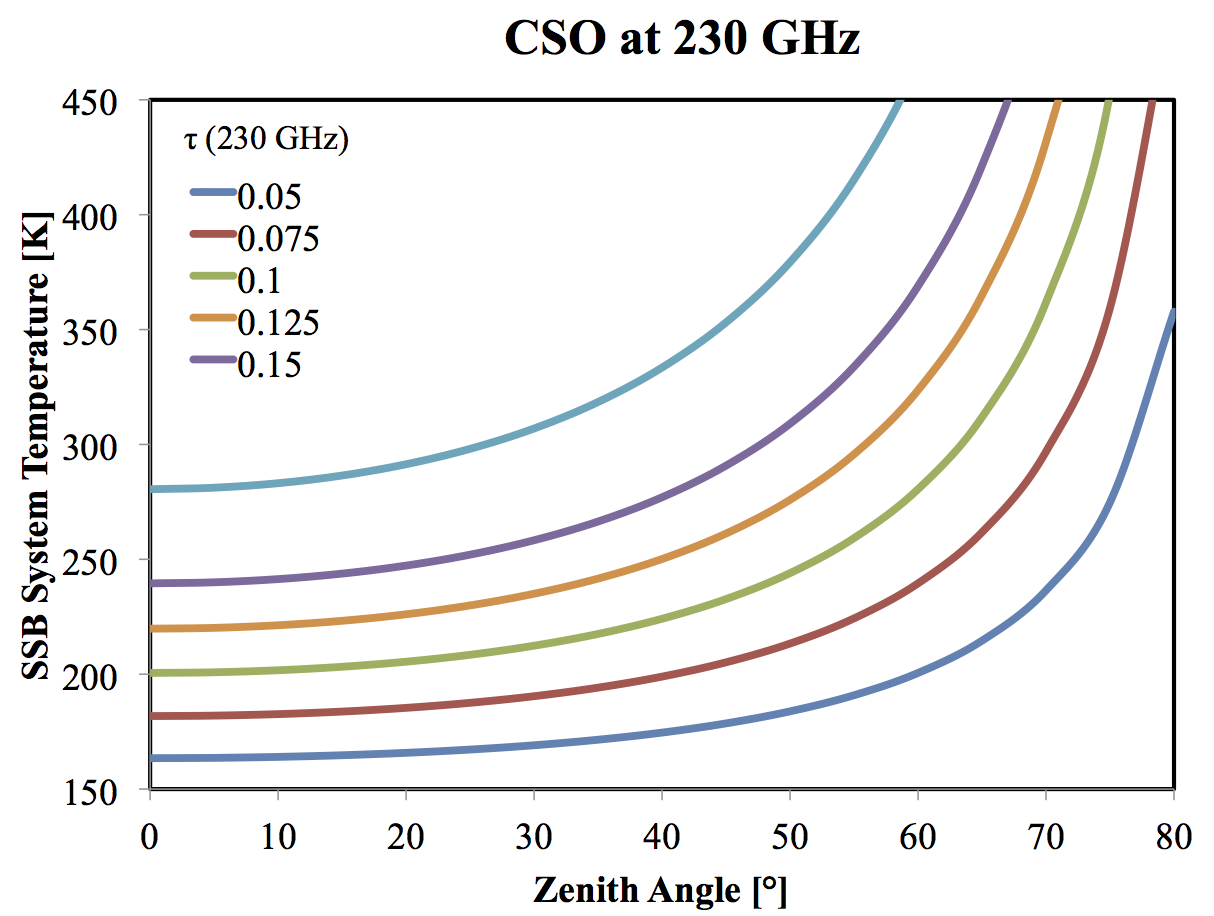
If you're observing small sources, further adjust for the main beam efficiency.
If the atmospheric optical depth in the two sidebands is different, please review the discussion of sideband correction.
